There are a couple of things that you need to know before you attempt to solve any exponential or logarithmic function:
Solving exponential equations using the one-to-one property
One-to-one property of logarithms:
One-to-one property of exponents:
We can use the one to one property to solve many of the logarithmic equations or exponential functions that you might run into.
Lets first look at an exponential equation to solve using the on-to-one property. Here is the equation:
When looking at this equation, the bases of both of the exponential terms is the same, 3. Due to the one-to-one property which states that is the bases are the same then the exponents must be the same, we know that the exponents are equal. That means that we have take away the bases and set the exponents equal to each other:
Now, we are left with a simple equation to solve. The final answer is:
Solving logarithmic equations using the one-to-one property
Now lets look at how you can use the one to one property of logs to solve a logarithmic equation, it is very similar to what we just did. Here is own equation:
According to the on-to-one property, since both logs have the same base, the arguments must be equal to each other. As a result, we can get rid of the logs and we are left with the arguments:
now that we have gotten rid of the logs, we are left with a simple equation to solve, the solution is:
Solving exponential equations by taking the log of both sides
You will be able to use the one to now property for many equations, and you can use it again to help you on many other ways, but there are occasions where you won't be able to use it, the equation below is a perfect example of one of those occasions:
Unless you know what to raise 10 by to get 46 off the top of you head, you need a way to isolate x so you can more easily solve this equation. Since this is an equation, you could do something to both sides and the equation would still be true. For example if I added 10 to each side, the equation would still be true. By that logic, if I took the log of both sides, or the natural log, the equation would still be true, so lets do that:
We know that the left side of the above equation is just equal to x, and the right side of the above equation stays the same. Now we have isolated x:
Now you need to plug this into your calculator, giving you:
*If you can't change the base of a log in your calculator, you can use the change-base formula
Solving exponential equations by exponentiation
The final way of solving logarithmic functions is by using exponentiation. That mean to make the entire equation an exponential equation. Lets start with this equation that we are trying to solve:
Now we can exponentiate both side, meaning that we make both sides of the equation the power to which a base, the same for both sides, is raised. We can technically make the base what ever we want, but it would make the most sense, and make it much easier, if we made the base 2. Here is what it looks like:
Although this new equation may look very different from the one before, due to the one to one property, it is still true. Now the on the left side, we can use the inverse property to simplify that to (x+4) and we can easily figure out what 2^3 if. Here is what the new equation looks like:
Now there is a simple equation to solve leaving x = 4.
Solving exponential equations in quadratic form
You may run across an equation that looks like this:
This may look familiar and it should. This looks very similar to a quadratic equation, especially when written like this:
Now we can factor this just as we would factor the equation:
This is what the equation looks like factored:
Now using the zero product property and then one of the properties from above we can easily find what x is.



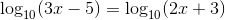













No comments:
Post a Comment