The graphs of sine and cosine functions represent their outputs for all real number values of a given angle, making the domain equal to all real numbers. The parent functions appear as shown below:
f(x) = sin x
f(x) = cos x
and
respectively, where the absolute value of a determines the amplitude of the function,
 determines the period, c determines the phase shift, and d determines the mid-line shift.
determines the period, c determines the phase shift, and d determines the mid-line shift.Definitions:
Amplitude: half the distance between the minimum and maximum values of the function. Variations in amplitude vertically stretch and compress the graph.
Period: one completed cycle of the repeating function. Increasing the value of b thus increases the frequency of periods in a given distance.
Phase Shift: Horizontal stretching and compressing.
Mid-line Shift: Vertical translation of the graph.
Cool things to note:
- The graph of f(x)=sin x is odd, as evidenced by the reflection about the origin.
- The graph of f(x)=cos x is even, which is seen in the symmetry about the x-axis.
- If one were to shift the sine graph
 units to the left, this phase shift represents the co-function identity:
units to the left, this phase shift represents the co-function identity: Examples:
Graph:
***It is important to realize that the period is
 and that the phase shift is 1/2. This becomes more evident once 1/2 is factored out of the parentheses. Otherwise, the amplitude is 2/3. Together, this determines the following graph (red) compared to the parent graph (blue):
and that the phase shift is 1/2. This becomes more evident once 1/2 is factored out of the parentheses. Otherwise, the amplitude is 2/3. Together, this determines the following graph (red) compared to the parent graph (blue):



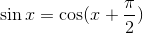










No comments:
Post a Comment