Inverse Trigonometric Functions
Inverse Sine Function
The graph of y = sin x does not pass the vertical line test due to the different values of x that have the same y value. However, if you restrict the doman to the interval -π/2 ≤ x ≤ π/2, it becomes a one-to-one function.
Now the inverse is possible to graph.
The domain of y = sin x (-π/2, π/2) becomes the inverse range and the range of y = sin x (-1, 1) becomes the inverse domain. This is called y = arcsin x.
Inverse Cosine Function
The graph of y = cos x does not pass the vertical line test due to the different values of x that have the same y value. However, if you restrict the doman to the interval 0 ≤ x ≤ π, it becomes a one-to-one function.
Now the inverse is possible to graph.
The domain of y = cos x (0, π) becomes the inverse range and the range of y = cos x, (-1, 1), becomes the inverse domain. This is called y = arccos x.
Inverse Tangent Function
The tangent graph is repetitive and therefore, the domain can be restricted to the interval (-π/2, π/2).
The domain of y = tan x (-π/2, π/2) becomes the inverse range and the range of y = tan x (-∞, ∞) becomes the inverse domain.
Notice that the vertical asymptotes of the y = tan x graph become the horizontal asymptotes of the y = arctan x graph.











 units to the left, this phase shift represents the co-function identity:
units to the left, this phase shift represents the co-function identity: 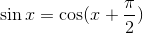









 and that the phase shift is 1/2. This becomes more evident once 1/2 is factored out of the parentheses. Otherwise, the amplitude is 2/3. Together, this determines the following graph (
and that the phase shift is 1/2. This becomes more evident once 1/2 is factored out of the parentheses. Otherwise, the amplitude is 2/3. Together, this determines the following graph (

























