Even and Odd Functions

Even Functions: 

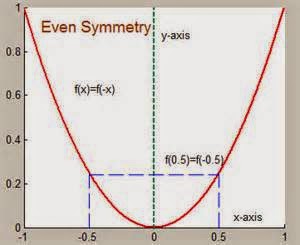
A function f is EVEN if, for each x in the domain of f,

f(-x) = f(x)

Properties:
-Symmetrical about the y-axis
-If point (x,y) is on the graph, then point (-x,y) is also on the graph

Examples: 
-the most common example is functions with even exponents
-parabolas are also an indicator of an even function

-another example is the graph of cos(x) which is also symmetrical about the y-axis

Odd Functions:

A function f is ODD if, for each x in the domain of f,

f(-x) = -f(x)

Properties:
-Symmetrical about the origin (0,0)
-If point (x,y) is on the graph, then point (-x,-y) is also on the graph 

Examples:  
- the most common example is functions with odd exponents

- another example is the graph of sin(x) which is symmetrical about the origin

How do you know if your function is even or odd?

Testing methods:

Graphically
-vertical line test will determine if the graph is a function = you should be able to draw vertical lines and each one should only run through one point exactly
-next, check to see if points (-x,y) & (x,y) are on the graph which would indicate an even function
-if that's not the case then check if points (x,y) & (-x,-y) are on the graph, which would be an odd function

Algebraically
-plug x into the function and then plug a -x into the function
-Even Example
f(x) = x² +1

plug in a positive x first      then      plug in a negative x
f(2) = (2)² + 1                                     f(-2) = (-2)² + 1
f(2) = 5                                               f(-2) = 5


Works Cited:
Cosine Function Graph. N.d. Www.calculatorsoup.com, n.p.Even Verse Odd Functions Graph. N.d. Www.intmath.com/functions, n.p.
Parabolic Graphs. N.d. Www.pic2fly.com, n.p.
Sin X Graph. N.d. Www.intmath.com, n.p.