Difference Quotients

What is the Difference Quotient and how does it work?

The Difference Quotient is 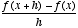. The Difference Quotient is used to find the secant slope of a line in which algebra can not be used to find the slope. Then by finding the secant slope, one can find the tangent slope to discover the slope of the point on the curved line. For now, we will just concern ourselves with the Difference Quotient.

Consider the graph above. In some situations, a mathematician would have to find the slope of the parabola. But there are infinite slopes to that parabola, so algebra can't really help here. First, you need to draw a tangent line like the one shown above connected to the point in which you want to find the slope.
The coordinates of your point are (x, y) or in our case (x, f(x)). To make a tangent line, you will need two points because every line requires two points.

 

 

The above picture shows the coordinates of the second point: (f(x+h), x+h). Using the change in y over the change in x (also shown above), you can see that the formula is  .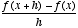

 

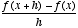Math Problems with the Difference Quotient

A very generic problem you will see is to find the Difference Quotient of a simple parabola, like in the picture above. Let's explore how to solve this problem.

 

The first part where it says "f(x+h)" take the formula for the parabola and substitute "(x+h)" everywhere for "x".

 

The second part where it says "f(x)", take the quantity of the formula of the parabola.

 

Write it all out and then simplify. MAKE SURE TO REMEMBER THE DISTRIBUTIVE PROPERTY.

 

Usually, you will have an opportunity to simplify and cancel out all of the h's. this is a sign you haven't made a silly mistake thus far.

 

Finally, simplify all of the way, and you will receive an answer like I did. If you receive '1' as your answer, that is a sign something went wrong. Go back and check your work (like you always should).