where N(x) and D(x) are polynomials and D(x) is not the zero polynomial.
In general, the domain of a
rational function of x includes all real numbers except
x-values that make the denominator zero
Example:
*Note: All polynomial functions are rational functions
Finding Intercepts
To find
the x-intercept:
An
x-intercept is when f(x)=0
Set the numerator equal to zero to find the x-intercept
N(x)=0
If D(x)=0, then F is undefined à
Vertical Asymptote
To find
the y-intercept
The
y-intercept is when x=0
Find the y-intercept by plugging in 0 for all values of x
F(0)=
Finding the Domain and Asymptotes
Definition
of Vertical and Horizontal Asymptotes:
1.
The line x=a is a vertical asymptote of the graph f if f(x)à∞ or f(x)à- ∞ as xà
a, either from the right or from the left
2.
The line y=b is a horizontal asymptote of the
graph of f if f(x)àb
as xà∞
or xà-∞
There is a vertical asymptote at x=3
Look at the leading terms and their coefficients: 2x and x. Do you have a big number over a little number? Do you have a little over a big? Are they the same? Now divide them:
There is a horizontal asymptote at y=2



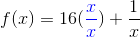







No comments:
Post a Comment