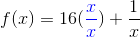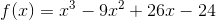Exponential Functions

Exponential Functions: A function where the base is a real number greater than zero, excluding one,
and the power is a variable. The variable is any real number and the base cannot equal one.

Correct Form

Incorrect Form

Polynomials often times get mixed up with exponential functions. Polynomials have the variable as the base while exponential functions have the variable as the power.

If the variable is negative then you take the function and place it in the denominator under one. 

Exponential Functions have a horizontal asymptote at Y=0 and the domain is always All Real Numbers. The graphs of exponential functions can be altered.

By adding D to the exponential function the graph will be shifted vertically

By multiplying A to the exponential function the graph will either be vertically stretched or compressed. If A is negative then the graph will be reflected over the X-axis.

By subtracting or adding C the graph will be shifted either right or left. 

By changing the base the graph will become either more or less aggressive. The larger the base the faster the graph will grow. When B is less than one the graph decays.  

The graph has moved five units upwards because five was added to the base. This created a new horizontal asymptote at Y=5. The graph was vertically stretched because the base was multiplied by five. 

Graphs of Rational Functions

How to Graph a Rational Function:

• Find the y-intercept by solving for f(0)
• Set the numerator equal to zero and solve to find the x-intercepts
• Set the denominator equal to zero and solve to find the vertical asymptotes
• Find and sketch any horizontal asymptotes
• Use smooth curves to complete the graph

Example:

First, find the y-intercept of the graph by moving for f(0), since f(0)= 2, the y-intercept is (0,2).
Then set the numerator equal to zero to find the x-intercepts:

         -1(x-2)=0

               x-2=0

                  x=2

The x-intercept is (2,0)

Next set the denominator equal to zero to find the vertical asymptotes. Since the denominator is in factored form we know that the vertical asymptote will be x= -1 because that is what makes it equal zero. We also know that the vertical asymptote will have a multiplicity of 2 because it is squared in the denominator. 

From the information previously gathered, we are able to come up with the above graph for the function. Note that the graph never crosses over negative one because it is the vertical asymptote and that towards the end of the graph, it curves up to meet the horizontal asymptote because the end behavior of the graph is restricted by the horizontal asymptote. 

Slant Asymptotes:

If the numerator of a rational function has a degree one more than its denominator, the graph of the function has a slant/oblique asymptote. 

Example:



To find the slant asymptote, use long division and divide  into , which results in .
y=x-2 would be the slant asymptote. Then graph the function like a normal rational function.

Notice that the graph approaches, but does not touch the line y=x-2

Works Cited

"Desmos Graphing Calculator." Desmos Graphing Calculator. N.p., n.d. Web. 19 Jan. 2015. 

Hostetler, and Edwards. "Graphs of Rational Functions." Precalculus with Limits a Graphing Approach. By Larson. Third ed. N.p.: Houghton Mifflin, n.d. N. pag. Print.

Rational Functions

A rational function can be written in the form:

where N(x) and D(x) are polynomials and D(x) is not the zero polynomial.

In general, the domain of a rational function of x includes all real numbers except x-values that make the denominator zero

 

Example:

Example:

 

 

 

*Note: All polynomial functions are rational functions

Finding Intercepts

 

                To find the x-intercept:

                                An x-intercept is when f(x)=0

                                               Set the numerator equal to zero to find the x-intercept

                                                                     N(x)=0

                                               If  D(x)=0, then  F is undefined à Vertical Asymptote

                To find the y-intercept

                                The y-intercept is when x=0

                                                Find the y-intercept by plugging in 0 for all values of x

                                                F(0)=

Finding the Domain and Asymptotes

                Definition of Vertical and Horizontal Asymptotes:

1.       The line x=a is a vertical asymptote of the graph f if f(x)à∞ or f(x)à- ∞ as xà

a, either from the right or from the left

2.       The line y=b is a horizontal asymptote of the graph of f if f(x)àb as xà∞ or xà-∞

 

                   

To find the vertical asymptote(s), set the denominator equal to zero

 

 

                        There is a vertical asymptote at x=3

 

 

To find the horizontal asymptote(s) of the graph, you must think about its end behavior (at the extremes)

     Look at the leading terms and their coefficients: 2x and x. Do you have a big number over a little number? Do you have a little over a big? Are they the same? Now divide them:

There is a horizontal asymptote at y=2

 

Sources

Precalculus with Limits. N.p.: Houghton Mifflin, 2001. Print.

The Fundamental Theorem of Algebra

Real and Complex Zeros of Polynomial Functions:
The Fundamental Theorem of Algebra states that if f(x) is a polynomial of degree n, where n > 0, f has at least one zero in the complex number system.

It can be determined from this, that in the complex number system, (real and non-real numbers) every nth-degree polynomial function has exactly n zeros.
For example, it can be determined that,

has precisely 4 total zeros, real and/or non-real, because the leading coefficient is 4.

The zeros that an nth-degree polynomial has can be all the same, can be all different, or can be a mixture of the two.

For example:

The function

has 3 zeros.  All of the zeros happen to be 2, therefore it has a multiplicity of 3.

The function 

also has 3 zeros.  These zeros are 2, 3, and 4, so they are all different, however.

The function

has 4 zeros.  Two of the zeros are 2, so 2 has a multiplicity of 2.  The other 2 zeros are complex numbers.  They are (2 + i) and (2 - i).

*It is important to note that when a function has a complex zero, in the form a + bi, the conjugate of that complex zero, a - bi, is also a zero in the function.  For example, if 5+3i is a zero, then 5-3i is a zero as well.

Graphs Showing Real and Complex Zeros of Polynomial Functions:

The Fundamental Theorem of Algebra can be shown in graphs as well.

In this example, 

 

is graphed.

It can easily be seen that this function has 4 zeros, just like it should.  These zeros are all real.

If this graph was moved down 4 units however, it would look like this:

In this graph, there are also 4 real zeros, but it is harder to see, because 0 has a multiplicity of 2, so the graph is tangent to the x-axis.

If the original graph was moved down 6 units, it would look like this:

This graph still has 4 zeros like the others, but only 2 are visible. This is because only 2 of the zeros are real, and two are non-real.  The graph has the opportunity to hit the x-axis twice more, but the it curves away from is before it reaches it, so those 2 zeros are imaginary.

If the original graph was moved up 4 units, if would look like this:

This graph once again still has 4 zeros, but all of them are non-real.  The graph has the opportunity to hit the x-axis 4 times, but every single time the graph curves away, so the zeros are all imaginary.

 Every time the graph curves away from the x-axis, it has the potential to hit the axis twice, therefore the non-real zeros have to be in conjugate pairs.

Finding the Zeros of a Polynomial Function:

First, graph the function,factor it, or use synthetic division to find its real zeros. Then take the remaining polynomial, after factoring out the real zeros, and find x when f(x) = 0.

The following will show an example of finding the zeros of a polynomial function:

Find the zeros of:

Using synthetic division, you can determine that -2 is a zero, and 1 is a zero with a multiplicity of 2.

The remaining polynomial should be:

Take this polynomial and find x when f(x) = 0.

2i and -2i are also zeros of the polynomial function.

Therefore the 5 zeros of the 5th-degree polynomial function are 2, 1, 1, -2i and 2i.

Finding a Polynomial with Given Zeros:

To find a polynomial with given zeros, just simply find the factors of the polynomial by writing x minus the zero for each zero, and multiply those factors together to get a polynomial function.

The following will show an example of finding a polynomial with given zeros:

The given zeros are -1, 3, and 4+2i.  Find a 4th-degree polynomial.

First, we know that since 4+2i is a zero, its conjugate pair, 4-2i must also be a factor.

To set up the function, convert the zeros into factors of the polynomial function, looking like this:

Which can be simplified to:

From there, just multiply the factors together to get the polynomial function.

The zeros of -1, 3, 4+2i, and 4-2i can be defined as the 4th-degree polynomial above.

Works Cited

"Desmos Graphing Calculator." Desmos Graphing Calculator. N.p., n.d. Web. 19 Jan. 2015.

Hostetler, Robert P., Bruce H. Edwards, and David C. Falvo. "The Fundamental Theorem of Algebra." Precalculus with Limits: A Graphing Approach. By Ron Larson. 3rd ed. Boston, NY: Houghton Mifflin, 2001. 182-86. Print.

Real Zeros of Polynomial Functions

Long Division of Polynomials

You can use long division of polynomials to find the real zeros of polynomial functions. For example:

Divide  by x-2.

 

Steps:

1.      Multiply (x-2) by 6x² to get 6x³. 

2.      Subtract.

3.      Multiply (x-2) by -7x to get -7x².

4.      Subtract.

5.      Multiply (x-2) by 2 to get 2x-4

6.      Subtract

You can use this solution to factor the function completely.  This is true by the remainder theorem, which states that if a polynomial f(x) is divided by x-k, the remainder is r=f(k).  In other words, if the remainder is zero, it as a factor and follows the factor theorem, which states that a polynomial f(x) has a factor (x-k) if and only if f(k)=0.

You can use this factorization to determine the zeroes of the polynomial function.

As you can see, the zeros of the function occur at 2, ½, and ²/₃.

Now what happens if you have a remainder other than zero?

If you have a remainder that is other than zero, you divide the remainder by the divisor and add it into the quotient.  For example:

This illustrates the difference algorithm which states that the dividend equals the divisor times the quotient times the remainder.

Important note – always make sure to use placeholders when there are missing terms in the dividend.  For example:

Synthetic Division

Synthetic division is a nice shortcut for long division; however keep in mind that it works only for dividing polynomials by divisors of the form x-k.  Here is an example:

Divide

Divideby x+3

Steps:

1.      Set up the array. Make sure to include placeholders when there are missing terms in the dividend.

2.      Drop the first number below the line and multiply it by the number in the upper left corner.

3.      Take the solution and put it above the line one place to the right.

4.      Add the two numbers above the line and write the product below the line.

5.      Repeat steps 2-5 until you have reached the final number

6.      If the final number is zero, there is no remainder.  If the final number is not zero, divide the remainder by the divisor and add it to the quotient.

A diagram of how the array is set up is shown below.

Rational Zero Test

The Rational Zero test relates the possible rational zeroes of a polynomial (having integer coefficients) to the leading coefficient and to the constant term of the polynomial.   The technical definition is if the polynomial

 has integer coefficients, every rational zero of ƒ has the form Rational zero=p/q where p and 1 have no common factors other than 2, p is a factor of the constant term a⁰,  and q is a factor of the leading coefficient aⁿ.  The rational zero test essentially tells us that the possible rational roots are the factors of the constant term divided by the factors of the leading coefficient. Here is an example of how to use the rational zero test to solve for the rational zeros of a polynomial: 

Normally when trying to solve for rational zeroes, you randomly plug in the possible rational zeroes and keep trying until one works.  This can be extremely lengthy and tedious.  Instead, if you graph the function on a graphing calculator, you will be able to calculate its zeroes by using the CALC function.  If the x-value is one of the possible rational roots, plug it into the upper left corner of the synthetic division array.  It will result in a zero remainder, meaning it factors cleanly and allows you to get onto the next step for synthetic division.  In addition, whenever the coefficients of a function add up to zero, (x-1) will always equal zero, meaning 1 is a zero of the function.

Works Cited

"Precalculus with Limits: A Graphing Approach." Precalculus with Limits: A Graphing Approach. N.p., n.d. Web. 15 Jan. 2015.