Tangent
The function f(x) = tan x can be rewritten as f(x) = sin x/cos x. The function of tan x has vertical asymptotes at the inputs that make cos x = 0 and x-intercepts at the inputs sin x = 0. The function has symmetry along the origin making it odd.
Domain:

Range:

Vertical asymptotes:

Period:

X-intrecepts:

Y-intercept: 0
Cotangent
The function f(x) = cot x can be rewritten as f(x) = cos x/sin x. The function of cot x has vertical asymptotes at the inputs that make sin x = 0 and x-intercepts at the inputs that make cos x = 0. The function has symmetry along the origin making it odd.
Domain:

Range:

Vertical Asymptotes:
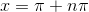
Period:

X-intercepts:

Y-intercept: none
Secant
The function f(x) = sec x can be rewritten as f(x) = 1/ cos x. The function of Sec x does not cross the x axis having a constant numerator of 1. It has vertical asymptotes at the inputs that make cos x = 0. Like the function of cos x the function of sec x has symmetry along the y-axis making it an even function.
Domain:

Range:

Vertical asymptote:

Period:

X-intercepts: none
Y-intercept: o
http://jwilson.coe.uga.edu/emt668/EMAT6680.2000/Umberger/EMAT6690smu/Day6/Day6.html
Cosecant
The function f(x) = csc x = 1/ sin x Like f(x) = sec x, f(x) = csc x does not cross the x axis having a constant numerator of 1. It has a vertical asymptotes the inputs that make sin x = 0. The function has symmetry along the origin making it odd.
Domain:

Range:

Vertical asymptote:

Period:

X-intercepts: none
Y-intercept: none



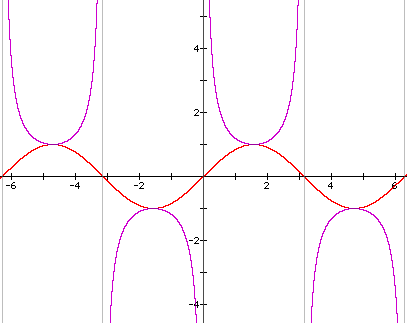











 units to the left, this phase shift represents the co-function identity:
units to the left, this phase shift represents the co-function identity: 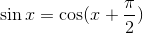









 and that the phase shift is 1/2. This becomes more evident once 1/2 is factored out of the parentheses. Otherwise, the amplitude is 2/3. Together, this determines the following graph (
and that the phase shift is 1/2. This becomes more evident once 1/2 is factored out of the parentheses. Otherwise, the amplitude is 2/3. Together, this determines the following graph (
















